Simulation of a 3D heterogeneous medium using the frequency-specific mixed domain method

This example shows how to simulate the wave propagation in 3D heterogeneous media with the frequency-specific mixed domain method. A skull-like medium and a flat transducer are modeled in this example. The input plane pressure is obtained from FOCUS to consider a baffled source (rigid boundary condition), as mSOUND currently only considers the pressure-release boundary condition. The transducer is circular and its diameter is 20 mm.

Defining the medium properties

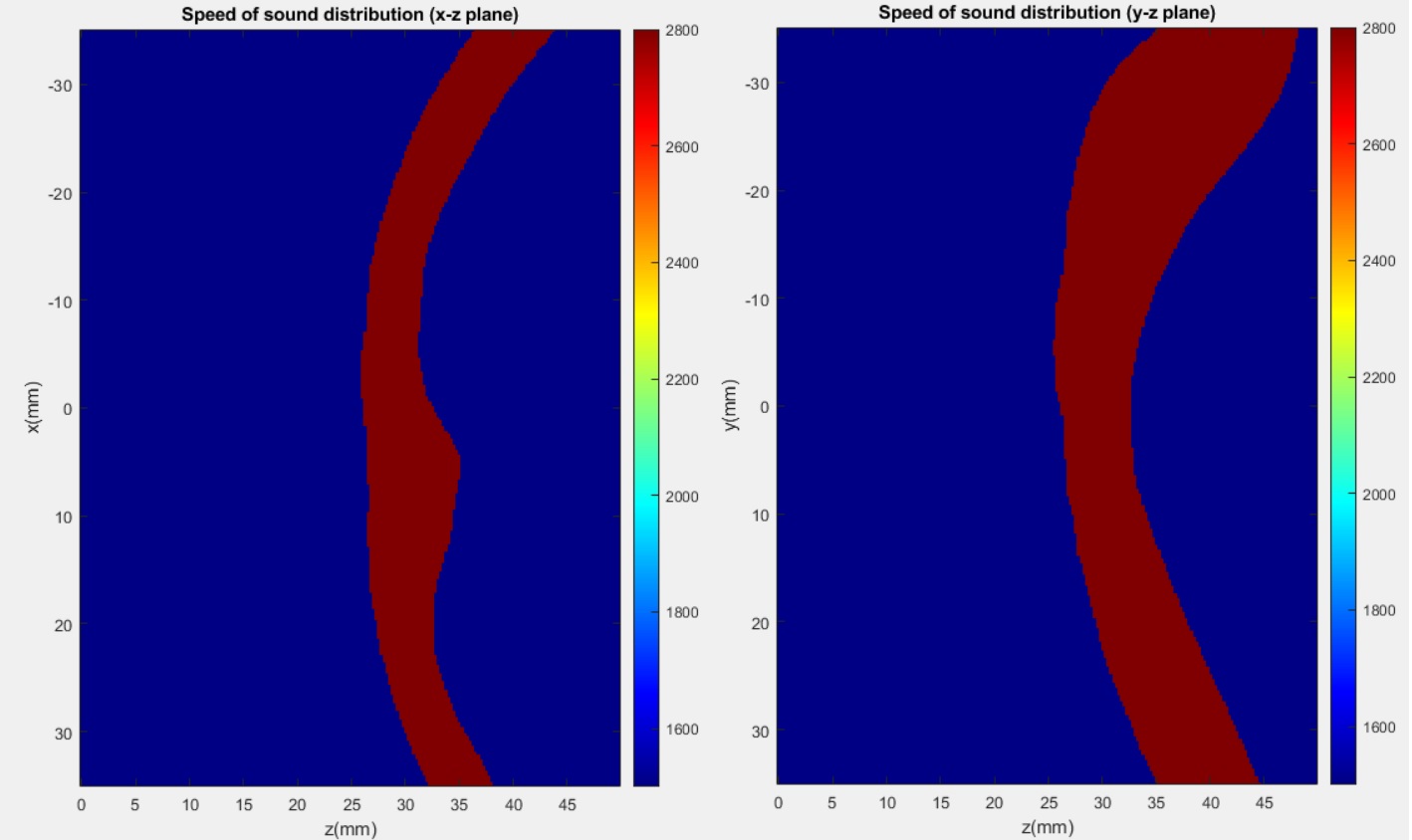
We first define the background medium and computational domain, and then load the skull data. Speed of sound distributions of the skull in the x-z and y-z planes are illustrated in the figure below. The speed of sound and density are assumed to be uniform inside the skull and are 2800 m/s and 1850 kg/m^3, respectively.

 

medium.c0 = 1500;      % speed of sound [m/s]
medium.rho0 = 1000;    % density of medium [kg/m^3]
medium.beta0 = 0;      % nonlinearity coefficient 
medium.ca0 = 0;        % attenuation coefficient [dB/(MHz^y cm)] 
medium.cb0 = 2;        % power law exponent

dx = lambda/12; % grid size in the x direction [m]
dy = lambda/12; % grid size in the y direction [m]
dz = lambda/12; % marching step size in the z direction [m]

x_length = 70e-3*4+dx;  % computational domain size in the x direction [m]
y_length = 70e-3*4+dy;  % computational domain size in the y direction [m]
z_length = 120e-3;      % computational domain size in the z direction [m]

% load the skull data
load skull_mask_dx_0.25mm.mat;

% define the non-reflecting layer
medium.NRL_gamma = 0.08;
medium.NRL_alpha = 0.01;

Excitation signal

This examples assumes a baffled source. Since mSOUND currently only models pressure release boundary, the pressure field on the input plane is generated using FOCUS. The FOCUS code is also included in the package.

  
load FOCUS_input_plane_unfocused_lossless_0.25mm.mat

3D forward simulation

The pressure field is calculated with the 3D forward simulation function Forward3D_fund. The optinal input "Correction" is applied in this example because both the speed of sound and density contrasts are large. Since only two velocities are present in this problem (1500 m/s for the background and 2800 m/s for the skull), "c_ref" is entered as [1500 2800].

 
reflection_order = 4;
% forward propagation of the fundamental frequency pressure   
p_fundamental = Forward3D_fund(mgrid, medium, source_p, omega_c,...
                reflection_order, [1500 2800], 'correction', 'NRL','single','riemann');

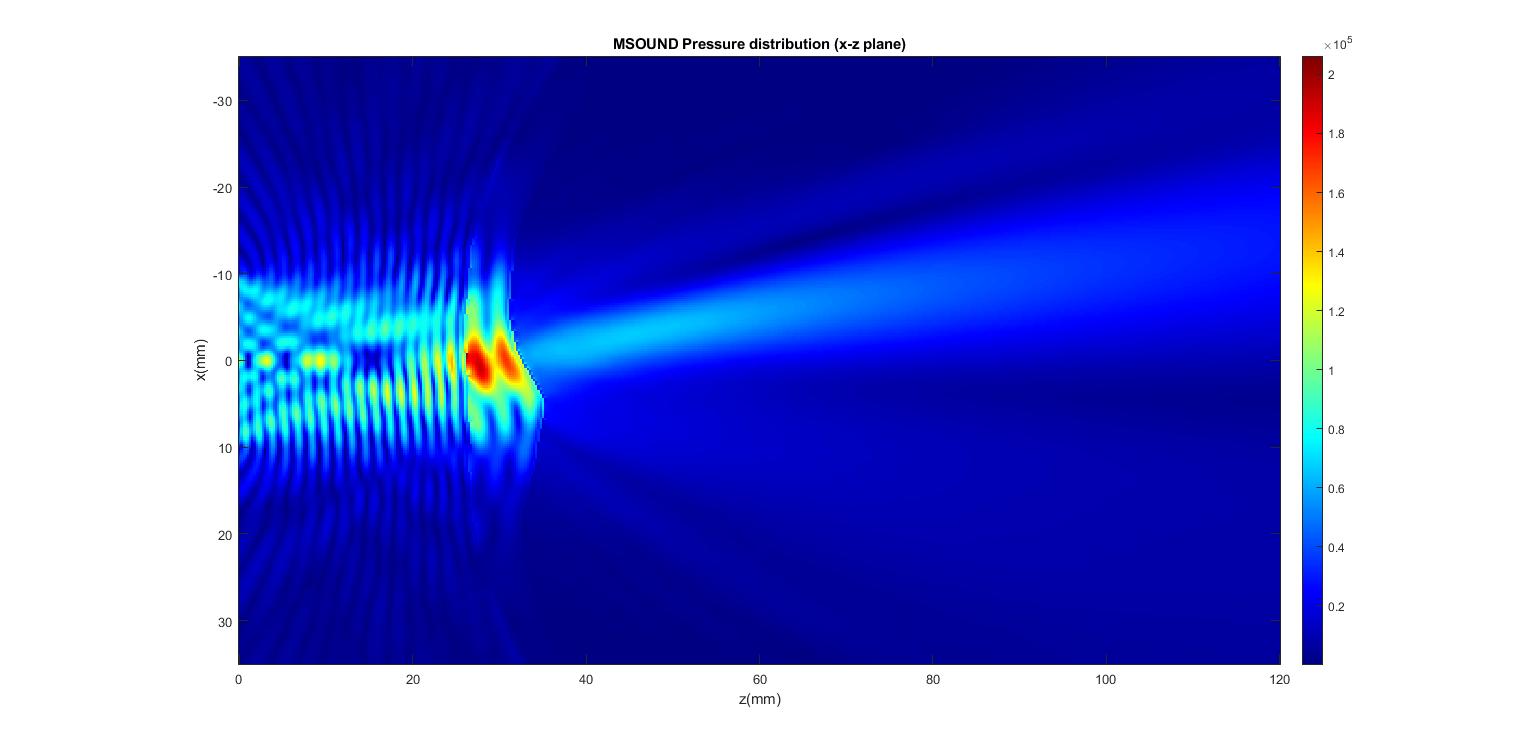
The figure below shows the pressure field on the x-z plane obtained by using mSOUND. fundamental and the fundamental pressure field

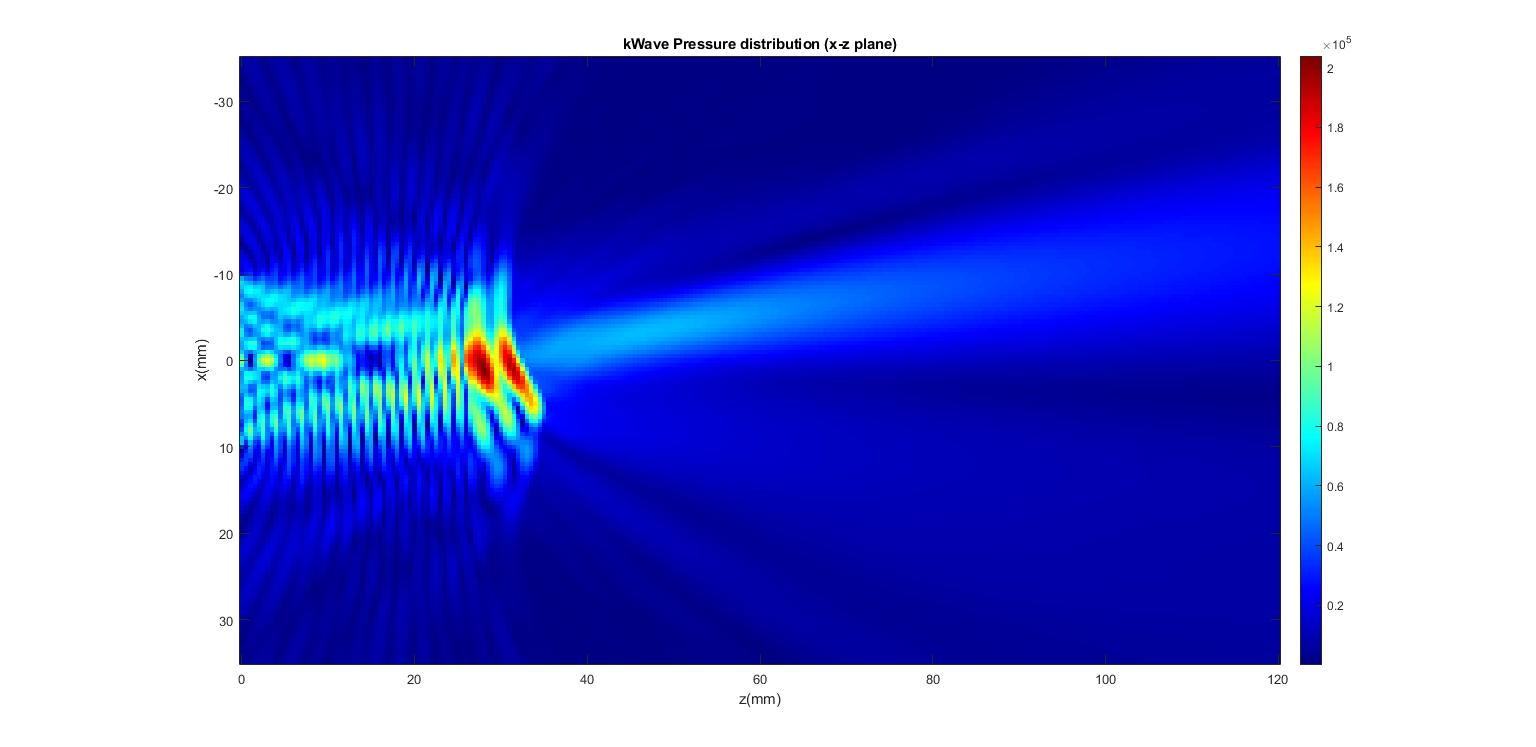
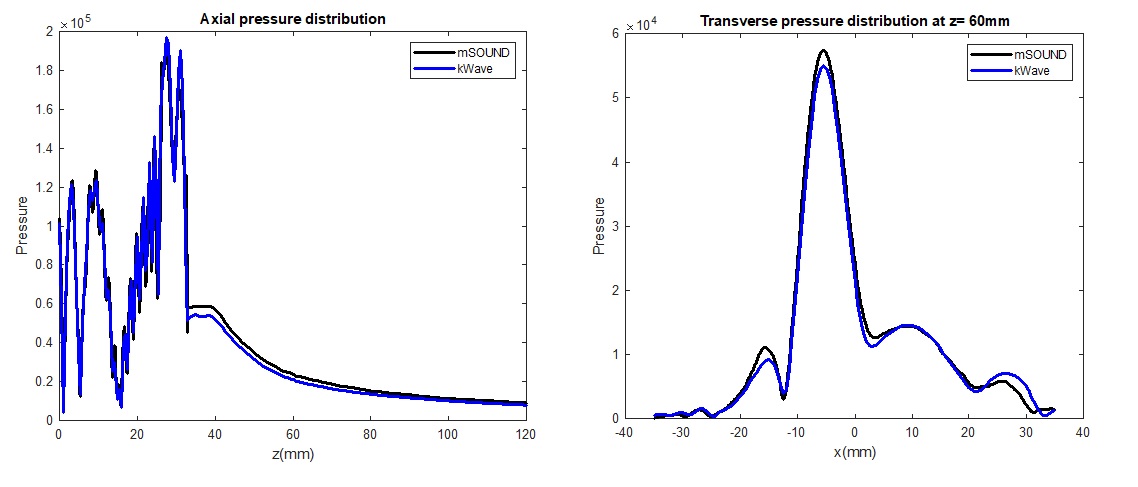
The figure below shows the pressure field on the x-z plane obtained by using kWAVE. fundamental and the second-harmonic pressure field

The figure below shows the pressure field distribution along the axial direction (x=y=0 mm) and transverse direction (z=60 mm). fundamental and the second-harmonic pressure field

Other examples